Informatik - 1

Das Konzept von Salts ist eigentlich ein sehr einfaches. Da ich jetzt aber ein paarmal über Menschen gestolpert bin, denen das Konzept nicht klar wurde (und es auch selbst am Anfang für etwas hoch-komplexes hielt), versuche ich mich mal an einer einfachen Erklärung.

Funktionsweise

Angenommen, man hat eine Webanwendung, in die sich Leute mit einem Passwort einloggen können (sie könnte Serendipity heißen). Selbstverständlich speichert man das Passwort dieser Nutzer nicht im Klartext ab, weil dann ein einfacher Blick in die Datenbank genügen würde, um das Passwort zu verraten. Stattdessen speichert man den Hash H des Passworts, der durch eine beliebige kryptographische Hashfunktion generiert wird:

H = hash(Passwort)

hash() ist im wesentlichen eine Einwegfunktion, also kann aus H nicht direkt Passwort rekonstruiert werden. Es existiert kein unhash(H) == Passwort.

Bei einem Loginversuch mit dem Passwort wird dann das Hashen wiederholt und mit dem gespeicherten H in der Datenbank verglichen:

bool loginCorrect?(passwort) {
    return (hash(passwort) == H)
}

Nur wenn die beiden Hashes übereinstimmen, stimmen die durch die Hashes repräsentierten Passwörter und der Nutzer kann sich erfolgreich einloggen.

Nun kommt der Salt dazu. Der wird zufällig gewählt, ist also eine zufällige Zeichenfolge, und wird dem Passwort angehängt:

hash(Passwort + Salt) = salted_H

Das wird nun bei jeder Passworterstellung gemacht, also insbesondere jedes Mal ein neuer Salt berechnet. Vom Prinzip her ist das alles.

Der Salt wird natürlich mit dem salted_H in der Datenbank gespeichert. Das ist notwendig, denn bei einem Loginversuch wird ja wieder ein Hash berechnet und mit dem gespeicherten verglichen:

bool loginCorrect?(passwort) {
    return (hash(passwort + Salt) == salted_H)
}

Warum?

Bleibt die Frage, warum man einen solchen Salt nutzen sollte. Die Antwort: Sicherheit. Es soll verhindert werden, dass aus den Hashes indirekt das Passwort berechnet werden kann. In der Konsequenz geht es um ein Gegenmittel gegen Rainbow-Tables.

Die Datenbank der Webanwendung könnte gestohlen werden, wie das ja in letzter Zeit reihenweise passierte. Ziel des Angreifers ist es danach, das Passwort im Klartext herauszufinden. Aus zwei Gründen:

1. Wenn er nur die Datenbank hat, könnte er sich dann in der Webanwendung einloggen und Aktionen durchführen
2. Viele Nutzer verwenden Passwörter mehrfach, sodass der Angreifer bei vielen anderen Diensten gültige Logins und Passwörter bekommen würden

Im Idealfall hat der Angreifer bisher nur die Datenbank mit dem Nutzernamen (der natürlich auch gehasht werden könnte), dem salted_H und dem Salt jedes Nutzers. Schon dank des Hashens reicht das nicht, um sich einzuloggen. Denn die Loginfunktion hasht ja wieder, gibt man den salted_H da ein entsteht also:

return (hash(salted_H + Salt) == salted_H))

Auch ohne den Salt wäre das false, denn man kann davon ausgehen, dass hash(hash(X)) != hash(X).

Ohne den Salt würde der Angreifer jetzt versuchen, eine Rainbow-Table aufzubauen. Dafür nutzt er seinen privaten Rechencluster in etwa so:

1000000000.times {
    passwort = guess_password()
    rainbow_table[hash(passwort)] = passwort
}

Er erstellt also eine Liste von gehashten Passwörtern und ihrem Klartext. Danach braucht er nur in der Datenbank zu schauen, ob der Hash verwendet wurde, und weiß deswegen, welches Passwort verwendet wurde um den Hash zu erstellen. Schon hat er das Passwort im Klartext.

Genau das verhindert der Salt. Da zwei Datenbanken oder sogar zwei Nutzer in einer Datenbank unterschiedliche Salts benutzen, unterscheidet sich ihr salted_H, selbst wenn sie das gleiche Passwort benutzen. Wird also eine Datenbank gestohlen, muss zwingend für jeden einzelnen Nutzer geguckt werden, ob

hash(guess_password() + Salt) == salted_H 

gilt. Eine Rainbow-Table, die die Salts mitspeichert würde absurd groß werden:

for salt in salts {
    1000000000.times {
        passwort = guess_password()
        rainbow_table[salt][hash(passwort +salt)] = passwort
    }
}

Daher kommt auch die Bewegung, teure Hashfunktionen wie bcrypt zu nutzen und sie möglichst noch mehrmals durchlaufen zu lassen. Bei einem Login ist die benötigte Zusatzzeit kaum bemerkbar, aber bei einem Knacken der Hashes tut jede ms weh.

Kurz

Ein Hash mit Salt ist einfach hash(X + Salt). Er schützt nicht generell vor schwachen Passwörtern, aber er erschwert es, dass Passwörter aus dem Hash rekonstruiert werden können.

Stanford bietet von September bis Dezember eine KI-Vorlesung als offene Online-Version an (via). Das Video zeigt ein paar der Inhalte:

Mich erinnerte es sehr an meine KI-Vorlesung. Klar, wir sind nicht mit Robotern durch die Stadt gefahren, aber die gezeigten Inhalte hatten wir größtenteils. Und er basierte auf dem gleichen Buch, was wohl wirklich das Standardwerk ist (Artificial Intelligence: A Modern Approach).
Was mir wieder klar machte, wie toll ich das Thema finde. KI ist nicht einfach eine simple Untermenge der Informatik. Wenn Informatik das Beherrschen von Informationen, das algorithmische Lösen von Problemen ist, dann ist das genau die Definition der KI. Die Algorithmen der schwachen KI haben mehr als andere den Ansatz, ein Problem generisch zu lösen statt es direkt lösen zu lassen, oder sind eher das Zusammenspiel von Algorithmen zur generischen Lösung eines Problems.

Beispiel Schach. Um dafür eine Lehrbuch-KI zu schreiben ist zwar Unmengen an Können notwendig, doch eigentlich braucht man "nur" eine eine performante Min-Max-Variante, plus den nötigen Optimierungen um der Komplexität beizukommen. In denen liegt dann die Schwierigkeit, aber Min-Max selbst ist ein sehr simpler Algorithmus, der einfach alle möglichen Varianten durchgeht und dann den Zug wählt, der für den Spieler das beste Ergebnis hat. Der Pseudocode hat 5 Zeilen.

Daher sah ich KI als praktisches Anwenden des Algorithmik-Kurses (der selbst schon ziemlich praxisbezogen war) und als Versuch, Probleme geschickt zu lösen. Da wird kein Data erschaffen, sondern Spiele gespielt, was nichts anderes als Problemlösen ist.

Und Problemlösen, darum geht es doch immer. Deshalb ist das Ansehen des Stanford-Kurs für die meisten Informatiker und Programmierer, die einen solchen Kurs noch nicht gehört haben, wahrscheinlich eine gute Idee.

Eines der neun von Turing vorweggenommenen Argumente gegen die Möglichkeit einer starken KI bezieht sich auf Ada Lovelaces Zitat:

It has no pretensions to originate anything. It can do whatever we know how to order it to perform.

Bei uns in der Diskussion darüber fiel der folgende Satz:

Ein Flugzeug kann auch besser fliegen als sein Ingenieur.

Fand ich treffend.

Bei dem Würfelspiel-KI-Wettbewerb vom Linuxmagazin hatte ich angekündigt, später mehr über meinen Ansatz zu schreiben. Denn der ist an sich simpel, funktionierte aber ganz gut - bis zu einer gewissen Grenze.

Statt auszurechnen, was die beste Lösung für das Problem ist, habe ich ein sehr simples Botmodell gebaut. Nochmal vereinfacht sah das so aus:

class DiceClient():
    def __init__(self, maxPoints, sprint, enemySprint):
        self.enemySprint = enemySprint
        self.maxPoints = maxPoints
        self.sprint = sprint

Er würfelte also und hatte zur Entscheidung, ob er weiterwürfelt, drei Merkmale bzw Grenzen. Wieviele Punkte ...

1. ... haben ich bereits in diesem Versuch erwürfelt
2. ... hat der Gegner insgesamt
3. ... habe ich insgesamt

Bei Erreichen der ersten Grenze speicherte er, bei Erreichen der anderen beiden versucht er, durchzuwürfeln um doch noch zu gewinnen.

Statt also nun diese Grenzen selbst möglichst optimal zu wählen, erstellte ich 20 solcher Bots mit zufälligen Werten und ließ sie spielen - gegen sich selbst, gegen andere Bots (von mir und von Freunden), gegen die Bots auf den Servern. Die Bots wurden nach ihrem Erfolg geordnet. Waren ein paar Spiele zusammen, ersetzte ein Kind der gewinnenden Bots einen der verlierenden. Dazu wurde die mutate() aufgerufen:

def mutate(self):
        random.seed()
        self.maxPoints = self.maxPoints + random.randint(-1,1)
        self.sprint = self.sprint + random.randint(-1,1)
        self.enemySprint = self.enemySprint + random.randint(-1,1)

Das Kind eines Bots war also eher kein identisches Abbild, sondern hatte leicht andere Werte. So sollte die Gesamtpopulation sich schrittweise den optimalen Grenzen annähern.

maxPoints: 30, sprint: 46, enemySprint: 48, generation: 23

Dieser Auszug aus der Speicherdatei beschreibt mein Endergebnis bei ungefähr 10000 Spielen mit diesem Botmodell, dabei habe ich es dann auch gelassen. Mit dem simplen, wobei schon erweiterten, Botmodell sind ein paar Konstrukte nicht ohne weiteren Umbau möglich gewesen die ich gerne als manuellen Startwert ausprobiert hätte, z.B. erst bis 16 würfeln, speichern, danach durchsprinten. Und dafür fehlte mir dann die Zeit.

Vor kurzem hat noch das Linuxmagazin seinen Würfelwettbewerb veranstaltet, jetzt richtet auch Google einen KI-Wettbwerb aus. Das Thema ist etwas anspruchsvoller (und attraktiver): Planetwars. Jeder Spieler hat Planeten, dort wachsen Schiffe, diese können losgeschickt und so neue Planeten erobert werden.

Die Auswertungreihenfolge bei (funktionalen) Programmiersprachen wie Scheme ist nicht automatisch gegeben. Beide Methoden im Titel haben Vorteile und Scheme z.B. nutzt im Standard die Applikative. Was bedeutet das überhaupt?

Applikative Reihenfolge: Erst Parameter auswerten, dann die Funktion ausführen.

Normale Reihenfolge: Die Funktion mit den unausgewerteten Parametern ausführen, dann die Parameter auswerten.

Applikativ

Im Klartext meint das folgendes: Eine Funktion wie + wird üblicherweise applikativ ausgewertet. Also würde ein Aufruf von

(2 + (5 - 3))

dazu führen, dass im nächsten Schritt dort

(2 + 2)

steht und dann mit diesen Parametern das gemacht wird, was die Funktion + damit nunmal machen will.

Normal

Bei einer bedingten Operation wäre das problematisch: Würden erst die Parameter ausgewertet, könnte es sein, dass die Prozedur überhaupt nicht mehr terminiert, z.B. dann, wenn eine Funktion sich selbst rekursiv aufruft - denn wie soll der Rekursionsanker getroffen werden, die Rekursion also zurücklaufen, wenn immer erst der Parameter ausgewertet wird? Ein Beispiel dafür wäre (die fiktive Funktion f in pseudo-Pseudocode)

f(n) {
if ( ( n  = 0 ) then 100 else f(n - 1) )
}

Hier sorgt die normale Auswertungsreihenfolge dafür, dass sobald n=0 ist die 100 ausgegeben wird, ohne dass der folgende elseteil ausgeführt wird, wodurch die Rekursion über die Parameterauswertung des if eben doch weiterliefe (weitere Beispiele).

Auswirkungen

Die normale Auswertungsreihenfolge ist immer dann notwendig, wenn mit Konstrukten wie Streams gearbeitet werden soll, die eben nicht immer vor der eigentlichen Betrachtung zuende aufgelöst werden können.

PS: Wikipedia nennt die Systeme strikte und verzögerte Auswertung.

Ein PDA ist ein Kellerautomat. Aus einer kontextfreien Grammatik kann man problemlos einen PDA erstellen. Dabei kommt man mit einem einzigen Zustand aus.
Ein Beispiel aus einer Grammatik:

S -> AX | BY | a

Um aus der Grammatik den PDA zu bilden geht man die Liste von oben nach unten durch und setzt sie in eine PDA-Zeile ein. Normalerweise hat man ja noch mehr zu übersetzen als nur das S, da A, X, Y und B auch noch zugeordnet werden müssen. Als Beispiel deckt das S aber jeden Fall ab.

Die Syntax:

(Zustand, Kellersymbol, Eingabe, Folgekellersymbol, Folgezustand)

Zuallererst wird ein Einstieg benötigt:

(q0, #, ?, S, q0)

Nun können die Zeilen der Grammatik angehängt werden, hier die S-Zeile von oben:

(q0, S, ?, AX, q0)
(q0, S, ?, BY, q0)
(q0, S, a, ?, q0)

An der Übersetzung kann man schon das ganze Schema ablesen. Die beiden q0 bleiben immer gleich. S ist das S von vor dem Pfeil.

An die dritte Stelle, die Eingabe, kommt das ?, wenn das betrachtete Zeichen noch weiter aufgelöst werden kann, dann kommt das Zeichen als Folgekellersymbol selbst in die vierte (so beim AX und beim BY gemacht).

Genau andersrum funktioniert es bei dem a: das kommt direkt in die Eingabe. Das ? füllt dann die vierte Stelle, ein echtes Folgekellersymbol gibt es in dem Fall ja nicht.

Diesem Schema folgend geht man nun die ganze Grammatik durch. Der Einstieg muss natürlich nur einmal gesetzt werden, ganz am Anfang.

Zusatz: Die so gebildeten Transitionen sind nur ein Teil des PDAs. Die Zustandsmenge Q und die akzeptierende Zustandsmenge A beinhalten aber nur {q0} - andere Zustände werden ja nicht angelegt. Das Kelleralphabet besteht aus den Zeichen vor den Pfeilen, hier also dem S.

Schritt 1: Umformen

{Q,¬A,¬B} := ((A & B)->Q)

{¬Q, ¬A,¬B}:=((A & B & Q)-> !T)

{Q}:=(T->Q)

M:= { {a,¬c}, {c}, {¬a, b, ¬c} } {¬b, ¬c, a, ¬d)

(c -> a) & (T -> c) & ((a & c) -> b) & ((b & c & d) -> a)

Schritt 2: Initialmarkierung

M1: (c¹ -> a) & (T -> c¹) & ((a & c¹) -> b) & ((b & c¹ & d) -> a)

Schritt 3: Whilemarkierung

M2: (c¹ -> a²) & (T -> c¹) & ((a² & c¹) -> b) & ((b & c¹ & d) -> a²)
M3: (c¹ -> a²) & (T -> c¹) & ((a² & c¹) -> b³) & ((b³ & c¹ & d) -> a²)
=> erfüllbar.

Schritt 4: Auswertung

   a   

   b   

   c   

   d   

   1   

   1   

   1   

   0   

Der Quicksort ist vom Prinzip schon sehr effektiv. Trotzdem kann er in natürlich optimiert werden, um den Wort-Case seltener eintreten zu lassen und die reale Performance zu erhöhen - nur wie? Welche Verfahren sind praktikabel, welche Kleinigkeiten kann man beachten?

Ich muss da selbst noch einiges lernen. Was mir aber bei meinen Versuchen bisher aufgefallen ist:

1. Kleinigkeiten nützen schon etwas. Wenn man nicht das mittlere Element als Pivot, sondern das linke oder das rechte wählt, dann kann man den jeweiligen Cursor auch links bzw. rechts vom Pivot ansetzen.

2. Noch eine Kleinigkeit: Beim Tauschen darauf achten, dass die zu tauschenden Elemente nicht sowieso schon gleich sind (evtl. ist das auch schlecht: kostet die Abfrage mehr Leistung als das unnötige Tauschen?)

3. Es gibt eine (relativ) naive Implementierung, bei der das linke, das mittlere und das rechte Element verglichen werden und der Mittelwert als Pivot gewählt wird. Wenn man die sowieso manuell betrachtet, kann man sie auch sortiert zurückschreiben: das kleinste nach links, das größte nach rechts, das Pivot in die Mitte.

Meinen bisherigen Tests nach hilft das enorm bei halbwegs geordneten Listen, schadet aber ein kleines bißchen bei komplett ungeordneten Zahlenabfolgen.

4. Wenn nur noch zwei Elemente in der zu sortierenden Liste sind, sollte das linke zum Pivot werden. Das kann aber natürlich auch eine Macke in meiner Implementation sein.

Noch testen will ich, wie es sich auswirkt, wenn man mehrere Threads nutzt und wie man das am besten anstellt.

Und sowieso: Ist es in der Realität nicht eher besser, auf die Kleinigkeiten zu verzichten und sich auf die Wahl eines guten Pivots zu beschränken, weil so Abfragen gespart werden - oder wiegen die gesparten Arrayzugriffe das wieder auf?

Auch wenn es mindestens die Hälfte meiner Leserschaft nicht wirklich interessieren wird, zeige ich hier mal wie man einen DFA per Hand (auch) minimieren kann. Das ist nämlich eigentlich recht einfach, solange der DFA simpel genug ist, wird aber oft genug kompliziert erklärt.

Nehmen wir folgenden DFA als zu minimierenden:

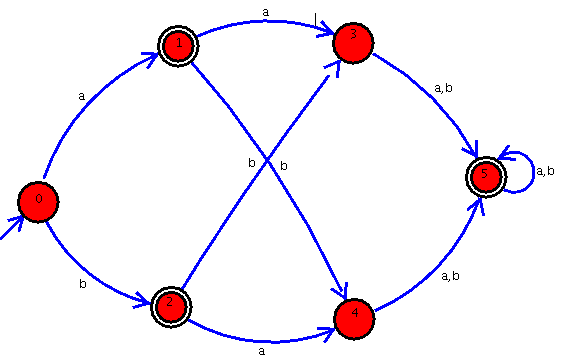
Minimieren kann nur funktionieren, wenn man überflüssige Zustände entfernt bzw. zusammenfasst. Am Anfang haben wir kein weiteres Unterscheidungsmerkmal als die Frage, ob die Zustände final sind (im Bild oben dargestellt durch die Doppelkreise) oder nicht. Grafisch betrachtet sieht das dann so aus (die Linien stellen die Übergänge dar, a ist blau, b braun, ab türkis)

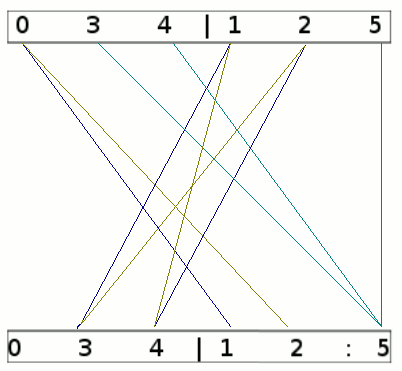
Der Doppelpunkt markiert das nächste Unterscheidungskriterium: Zustand 1 und 2 gehen über a bzw. b in die linke Gruppe, Zustand 5 geht jeweils in sich selbst, also in die rechte Gruppe: Hier kann innerhalb der Gruppe "125" nochmal unterschieden werden zwischen "12" (gehen beide in die linke Gruppe) und "5" (geht in die rechte Gruppe).

Nun sieht der nächste Schritt so aus:

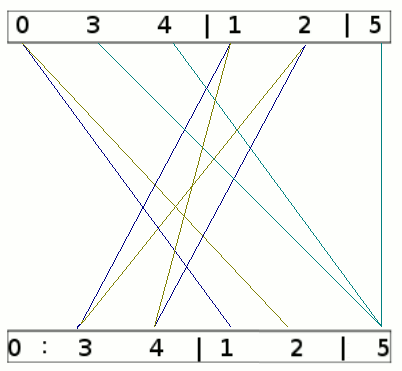
Da 3 und 4 nun auf eine andere Gruppe als 0 zeigen, kann jetzt auch in der linken Gruppe unterschieden werden.

Führt man das Verfahren nun nochmal aus, zeigt jedes Gruppenmitglied auf die gleiche Gruppe, ein weiteres Unterscheiden ist also nicht möglich.

Der fertig minimiert DFA sieht also wie folgt aus:

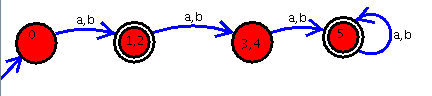
PS: Die DFAs wurden mit dem Automaton Simulator gezeichnet.