Wächst das Internet exponentiell?
Sunday, 24. March 2013
Die Telekom will Trafficbegrenzungen für normale DSL-Anschlüsse einführen, so geht es derzeit durch die Medien. Und auf dem Telekom-Blog wird dazu ein Nicht-Dementi veröffentlicht, das nur sagt, dass solche Tarife noch nicht eingeführt wurden, ohne Distanzierung von diesen Plänen. Verwiesen wird dabei auf einen Spiegel-Artikel mit den Worten:
Auf der einen Seite wächst das Datenvolumen exponentiell.
Doch stimmt das? Der Spiegel-Artikel gibt das gar nicht so einfach einfach her.
Definition: Wachstum
Was bedeutet exponentielles Wachstum überhaupt? Bei exponentiellem Wachstum wächst etwas immer stärker, je mehr da ist, um einen festen Prozentsatz. 2^x wäre eine solche Wachstumsfunktion: 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024 ... Man muss sich klarmachen, dass dies bei großen Werten im realen Leben extrem katastrophal sein kann - z.B. beim Ölverbrauch. Hätten wir einen festen Ölvorrat und wüchse unser Verbrauch exponentiell, stünden wir irgendwann an dem Punkt, an dem am nächsten Tick der gesamte verbliebene Ölvorrat verbraucht würde - genau das macht das Peak-Oil-Szenario so erschreckend.
Lineares Wachstum ist einfacher. Wächst etwas immer um den gleichen Wert, wächst es linear - beispielsweise wenn jemand jeden Tag eine Liegestütze mehr macht.
Polynomiales (kubisches) Wachstum (meine Vermutung: Internetwachstum entspricht eher sowas) sieht exponentiellem Wachstum ähnlich, hat aber nicht diese enorme Steigerung am Ende des Graphen. x³ ist das Beispiel im Graphen: 1, 8, 27, 64, 125, 216, 343, 512. Etwas, das immer mehr immer mehr wird, jedoch später mit immer geringerem prozentualem Wachstum.
Trafficentwicklung des Internets
Der Spiegel-Artikel gibt das exponentielle Wachstum also gar nicht so einfach her. Denn der fasst die Studie so zusammen:
Bis 2016 werde sich das durch die weltweiten Computernetze transportierte Datenvolumen vervierfachen
Eine Vervierfachung ist aber noch nicht exponentielles Wachstum. Exponentielles Wachstum ist irgendwas^x, eine Vervierfachung ist 4*x. Man sieht mein Problem auch schön auf dem (per Cisco-Tool) erstelltem Graph der Trafficprognosedaten:

Die Linie für z.B. Nordamerika sieht linear aus. Ist das im gesamten wirklich exponentielles Wachstum?
Hier noch die Daten des Gesamttraffics aus dem Whitepaper per Wolfram:
Das sind 30.734, 43.441, 54.812, 69.028, 87.331, 110.282 PB per Monat.
Und immerhin: Das Wachstum erhöht sich im Laufe der Zeit. Jährlich wächst der Traffic um 13, 11, 15, 18, 23 PB per Monat. Lineares Wachstum können wir also ausschließen. Aber ist das nun exponentiell oder polynomial?
Sieht man das am Steigungsgraph der Interpolation?
Ich nicht.
Exponentielles Wachstum ist Wachstum um einen festen Prozentsatz. Und prozentual ist das bei den gegebenen Werten Wachstum um 43%, 25%, 27%, 26%, 26%. Das ist also praktisch exponentielles Wachstum, abgesehen von der Abweichung im ersten und zweiten Jahr. Die prozentualen Wachstumswerte als Chart:
Nebenbei: Mathematisch erschlagen
Hier hatte ich zuerst die Interpolation genommen und mir mit großen x angesehen. Aber eine Interpolation per Polynom kann doch nur polynomiales Wachstum zeigen, oder? Und Wolfram kann auch nicht einfach die Fortsetzung dieser Reihe berechnen, was ich einfach mal als Hinweis auf nicht-exponentielles Wachstum nahm.
Man kann auch versuchen, das per Hand zu berechnen. Und vergessen wir dabei einfach mal den Wachstumsabfall - es geht also um das Wachstum 11, 15, 18, 23 der Werte 43, 54, 69, 87, 110.
"Es gibt ein m>1, so dass für n>=n_0 stets (a_n+1)/(a_n) >=m ist, dann liegt exponentielles Wachstum vor (man zeigt leicht a_n>= C m^n)"
-
- 54/43 >= m
- 69/54 >= m
- 87/69 >= m
- 110/87 >= m
Ja, ein solches m existiert:
Demnach wächst das Internet exponentiell. "Gibt es M>0 und p mit: für n>=n_0 ist stets a_n>M n^p, dann hat man mindestens polynomiales Wachstum."
Das ist auf deutsch die simple Überlegung: Finden wir ein Polynom, das weniger stark wächst als die gegebenen Werte?
Gut, prüfen wir das. Das zu lösende Gleichungssystem:- 43 > M * 1^p
- 54 > M * 2^p
- 69 > M * 3^p
- 87 > M *4^p
- 110 > M * 5^p
Und ja, solche p und M scheinen zu existieren:
"Gibt es M und p mit: für n>=n_0 ist stets a_n<=M n^p, dann hat man höchstens polynomiales Wachstum."
Finden wir ein Polynom, das stärker wächst als die gegebenen Werte?
- 43 <= M * 1^p
- 54 <= M * 2^p
- 69 <= M * 3^p
- 87 <= M *4^p
- 110 <= M * 5^p
Und ja, auch solche M und p gibt es:
Demnach wächst das Internet nicht exponentiell, sondern polynomial.
Und dadurch wird klar: Diese Formeln sind für echte Folgen, nicht für ein paar Werte, und helfen hier nicht weiter. Sie sagen nur, dass man die Werte sowohl exponentiell als auch polynomial fortsetzen kann.
Trafficentwicklung in Deutschland
Aber es geht in der Diskussion um Volumenbegrenzungen für DSL-Anschlüsse ja gar nicht um das ganze Internet. Es geht um DSL-Anschlüsse in Deutschland, und ohne mobiles Internet, ohne die Internetisierung der Entwicklungsländer, kann das alles ja schon wieder ganz anders aussehen. Oben im Cisco-Graph sah das Wachstum für Deutschland sehr linear aus.
Aber es geht ja ein bisschen genauer.
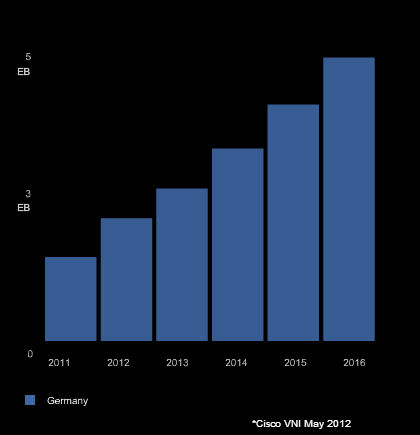
Aus der Advanced-Version des Cisco-Tools kommen die genauen Daten: Traffic bis 2016 ohne mobiles Internet und nur für Deutschland. Zugunsten der Telekom mische ich Business und Consumer-Segment, auch wenn es bei diesen Tarifen wahrscheinlich nur um Consumer gehen wird (so ganz sicher kann man sich eben nicht sein). Das sieht so aus
Die genauen Werte sind 1196.9, 1748.6, 2175.3, 2744.6, 3370.2, 4040.4. Das Wachstum also 552, 427, 569, 626, 670. Wieder sich steigerndes Wachstum, abgesehen von dem Einbruch auf 2013. So sieht die Ableitung der Interpolationsfunktion aus (interessante Abweichung):
Das ist Wachstum um 46%, 24%, 26%, 22%, 19%. Also: Nein, bei dem Wachstumsabfall am Ende ist das eher kein exponentielles Wachstum, sondern polynomiales.
Als Chart:
Fazit
Zuerst: Ja, die Cisco-Daten sagen aus, dass das Internet insgesamt exponentiell wächst (wenn Internet == Traffic). Nicht jedoch das deutsche Internet ohne Mobilfunk, um das es bei der DSL-Volumenbegrenzungsdiskussion geht. Aber auch das deutsche Internet wächst nicht linear, sondern es wächst der Prognose nach von 26% bis 19% im Jahr, was immer noch gewaltiges Wachstum ist. Das könnte für die Telekom tatsächlich eine Herausforderung sein - um das richtig zu bewerten müsste man die Kapazitäten kennen. Trotzdem deuten die Daten daraufhin, dass sich die Situation für die Telekom im DSL-Bereich in Zukunft eher entspannen wird, wenn das prozentuale Wachstum tatsächlich weiterhin abnimmt. Dementsprechend halte ich den simplen Hinweis auf exponentielles Wachstum des Internets für irreführend.
PS: Danke an Robert und Hartmut für eure Hilfe beim Erstellen des Artikels.